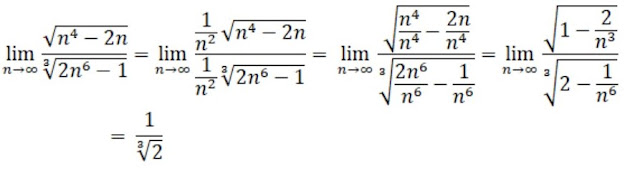EJERCICIOS SOBRE LÍMITES RESUELTOS

EJERCICIOS RESUELTOS DE LÍMITES

 

 EJERCICIOS DE LÍMITES AL INFINITO RESUELTOS

Debemos recordar: c/0 = ∞, 0/c = 0, ∞/c = ∞, c/∞ = 0

NOTA: al dividir en una fracción para la misma expresión tanto al numerador como al denominador la fracción no se altera.

En algunos límites al infinito se puede seleccionar a la variable con la mayor potencia, ya que al ser el infinito elevado a una potencia, mientras mayor sea el exponente, más rápido crecerá al infinito.

En el ejercicio 1, numerador y denominador tienen a la variable y a su exponente iguales. Se divide para n cada término del numerador y denominador.

En los ejercicios 2 y 3 se selecciona la variable con mayor potencia y a cada término del numerador y denominador se divide para esa variable.

EJEMPLOS CON RADICALES EN LAS FRACCIONES

EJERCICIO 4. Analicemos en el siguiente límite:

• Si n =10 → f(n) = 1.015
• Si n = 100 → f(n) =0.8791
• Si n = 1000 → f(n) =0.8673
• Si n = 10000 → f(n) =0.8662

Nos damos cuenta que el valor del límite se acerca cada vez más al obtenido en el ejercicio 4.

EJERCICIO 5. Analicemos en el siguiente límite:

• Si n =10 → f(n) =0.7929
• Si n = 100 → f(n) = 0.79369
• Si n = 1000 → f(n) = 0.7937005